Semantics modelling of systems

Semantics modelling of systems

Frédéric Herbreteau, Bordeaux INP/LaBRI (frederic.herbreteau@bordeaux-inp.fr)

What is a model?

bg left:33% fit

  • abstract representation of an object or a phenomenon
  • view of selected features or parameters of the object / phenomenon
  • with a specific goal of understanding its properties

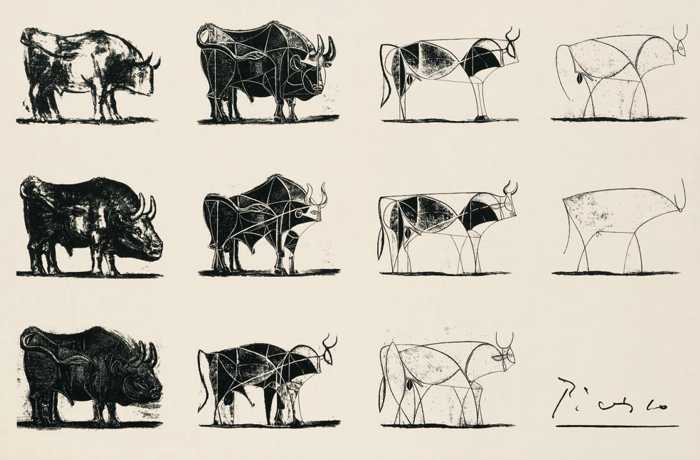
Abstraction is an art

“Le taureau”, Pablo Picasso, 1942

A model of a house

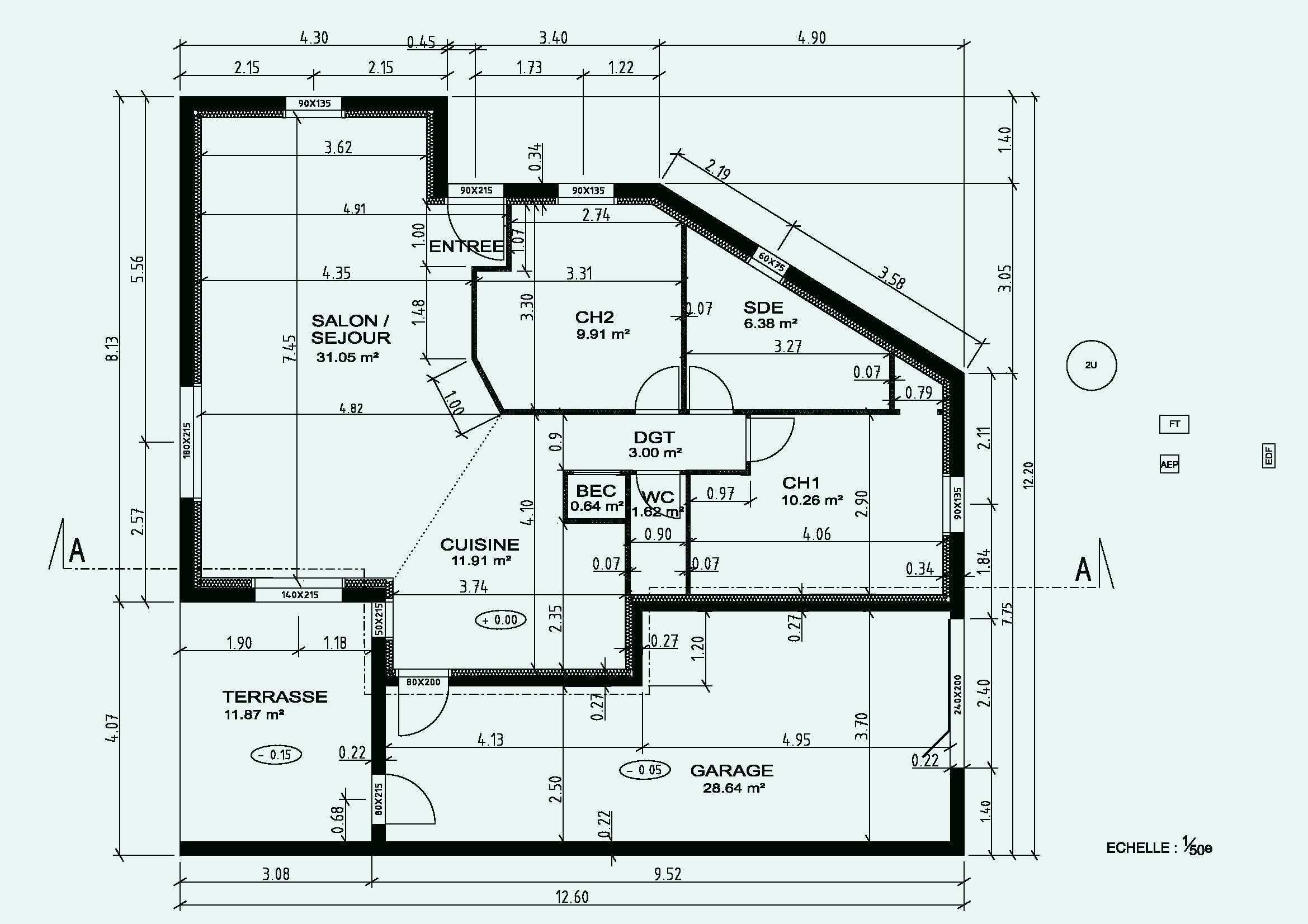
bg left:50% fit

  • precise information to build the walls
  • but not for electrical wiring

Another model of a house

bg right:50% fit

  • good for selling the house
  • no relevant information to build it

Models for software engineering

Many aspects to describe, with dedicated models:

  • class diagram: software architecture
  • deployement: placing components on nodes
  • use cases: users and tasks
  • activities: control flow to achieve a task
  • state diagram: evolution of an object during its lifetime
  • sequence diagram: interactions between components to achieve a task
  • …

UML is one (informal) notation (among many others) to build such models

Expectations for a model for software verification

What properties do we want to check?

  • The program terminates / does not terminate
  • The computed value is correct
  • A sequence of events is correct
  • Mutual exclusion
  • No deadlock
  • …

We need a formal model of the runs of a program (or a system)

Modeling the behaviors of a system

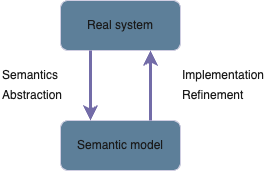
bg right:40% fit

Semantics model = formal representation of:

  • the states of the system
  • the stepwise behavior
  • the initial states
  • and state properties

Transition systems and runs

A transition system (or state machine) $T = (S, S_0, \to, AP, L)$ is defined by:

  • $S$ is the set of states with initial states $S_0 \subseteq S$
  • $\to \subseteq Q \times Q$ is a transition relation
  • $AP$ is the set of atomic propositons (i.e. state labels)
  • $L$ labels each state in $S$ by a subset of $AP$

A run is a (potentially infinite) sequence of states: $s_0 s_1 \cdots s_n \cdots$ such that $s_0 \in S_0$ and $s_i \to s_{i+1}$ for every $i \ge 0$

Example: drink vendor machine

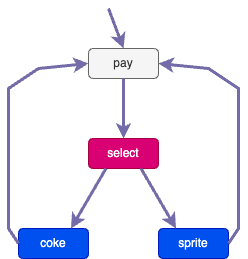
bg left:33% fit

What is abstract in this model?

  • Consider $AP=\lbrace \textcolor{blue}{\bullet}, \textcolor{red}{\bullet} \rbrace$

Characterize runs that satisfy:

  • “every paid drink is served”?
  • “every served drink has been paid”?

Do the runs of this model satisfy these properties?

Example: a digital circuit

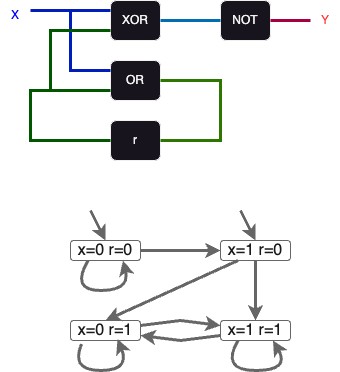
bg left:40% fit

  • output function: $y = \neg (x \oplus r)$
  • transition function: $\delta_r = x \lor r$
  • initial register value: $r = 0$

What is abstract in this model?

Run on input: $010100$?

  • Consider $AP = \lbrace 0, 1\rbrace$

Label states such that it matches output

Example: concurrent program

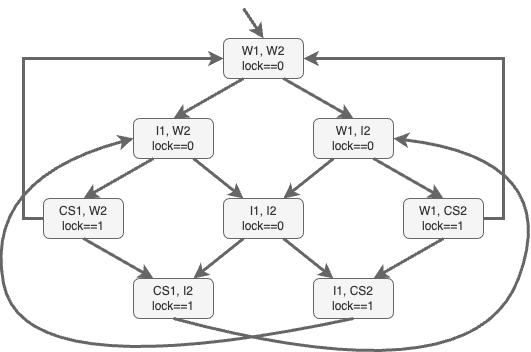
bg right:45% fit

shared bool lock = 0;

process:
  while (true):
    if (lock == 0) then lock := 1
    // critical section
    lock := 0

What is abstract in this model?

  • $AP=\lbrace req_1,cs_1,req_2,cs_2\rbrace$

Characterize runs that satisfy:

  • mutual exclusion
  • absence of starvation for $P_1$

Conclusion

  • transition systems are
    • a semantics model that yields a formal representation of the behaviors of a system
    • easily manipulated by algorithms (extensions of graphs)
  • In practice, transition systems are described using high-level formalisms (BPMN, PlusCal/TLA+, extended automata,…)

Any verification using model-based techniques is only as good as the model of the system