Introduction to formal design of software

Introduction to formal design of software

Frédéric Herbreteau, Bordeaux INP/LaBRI (frederic.herbreteau@bordeaux-inp.fr)

Is this program correct?

def fact(n):
   return 1 if n == 0 else n * fact(n - 1)

• What does it mean?
• How to assert it?

Some examples where it matters

Therac-25 Radiation Overdosing (1985-87)

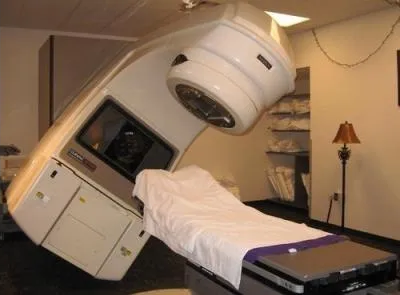
• Radiation machine for treatment of cancer patients
• At least 6 cases of overdoses in the period 1985-1987
• Three death cases
• Issue: design error in the control software (race condition)

Pentium FDIV Bug (1994)

• FDIV= floating point division unit
• 1 in 9 billion floating point dividers would produce inacurate results
• Cost: 500 million US$ in replaced processors
• Issue: flaw in a division table

Ariane V crash (1996)

• Cost: more than 500M US$
• Issue: data conversion from 64-bit floating to 16-bit signed integer

BOEING 737-MAX (2019)

• 356 people died (2 crashes)
• Cost: tenths of billion US$
• Issue: design of the flight control software (MCAS)

911 Outage (2020)

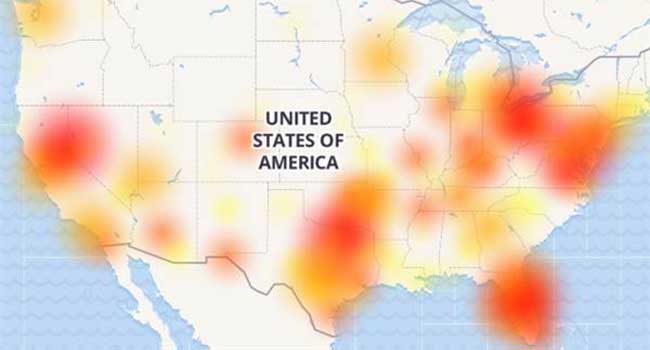
• 911 emergency call unavailable for ~1h
• Patients at risk:
  • heart attack: 1h-3h
  • low oxygen saturation: <1h
  • acute bleeding: <1h
• Issue: hard limit on an incoming-calls of 40 million (new calls dropped)

Also in 2014, 2018, 2019

Why it is difficult to verify computer systems?

• Big number of components interacting together
• Intrication between components (lack of abstraction at the specification or code level)
• Focus on programming languages instead of mathematical concepts behind
• Some bugs are difficult to detect with widespread development techniques (code reviews, testing, etc)

Main causes that lead to software bugs

• Almost all errors were due to flaws in specification and not in coding
• Reliability techniques (like redundancy) not effective for software
• Assuming the risk decreases over time
• Revision for undesired behaviours is very productive
• Software reuse without safety analysis
• Unnecessary complexity of software

(source: “The role of software in recent Aerospace Accidents”, Nancy G. Leveson Aeronautic and Astronautic Department MIT)

Formal verification at work

The transputer project

• Processors for parallel computing (notably used in GPS)
• formal development of T800 FPU
• formalisation revealed issues: diagnostic information should be propagated, but it was impossible sometimes
• Queen’s Award for Technological Achievement (1990)

Provably secure cryptography

• Everest project
  • verified implementations of protocols behind https (TLS, etc)
  • secure software actually deployed (Linux, Azure, Firefox, etc)
• Cryptoline project
  • tool and a language for the verification of low-level implementations of mathematical constructs
  • verified implementations in OpenSSL, mbed TLS, etc
• Fiat-Crypto
  • synthesizing correct-by-construction code from cryptographic primitives

Paris metropolitan 14

• Driveless train system: automatic control and signaling
• Developed using B-method
• B: 115.000 lines, 27.800 lemmas
• Ada: 86.000 lines
• Automatically proven: 92%
• Time to develop: ~4 years
• Bugs development & tests: 0
• Bugs since deployment: 0

Amazon Web Services

• In 2013, S3 is 2.000.000.000.000 (2 trillions) objects, 1.1 million requests/second
• Standard “verification” techniques in industry: Deep design reviews, Static code analysis, Fault-injection testing, …
• DynamoDB: scalable, high-performance, high-availability storage
  • Informal proofs already found bugs
  • Formalization in TLA+ revealed a very subtle bug in the full fault-tolerance algorithm (has passed all reviews, 2 other bugs found later)
  • New features are now first modeled and checked in TLA+

human intuition is poor at estimating the true probability of supposedly “extremely rare” combinations of events

Return on experience (AWS)

[…] help engineers to get the design right. […] If the design is broken then the code is almost certainly broken. Coding mistakes extremely unlikely to compensate mistakes in design.

[…] gain a better understanding of the design. […] can only increase chances that they will get code right.

[…] write better assertions […], a good way to reduce errors in code. Formal methods help engineers to find strong invariants, so formal methods help to improve assertions, which help improve the quality of code.

(source: Chris Newcombe, Rath Tim, Fan Zhang, Bogdan Munteanu, Marc Brooker, and Michael Deardeuff. Use of Formal Methods at Amazon Web Services. 2014)

CompCert

• Buggy compilers may silently introduce errors in otherwise correct programs

We have randomly generated C programs, and used them to find compiler bugs. So far, we have reported >325 previously unknown bugs. Every tested compiler has been found to silently generate wrong code on valid inputs (source: PLDI’11)

• CompCert: formally verified, realistic C compiler with optimizations

Semantic preservation theorem: for any source program S, if the compiler applied to S produces code C without reporting a compile-time error, then the observable behavior of C is one of the possible observable behaviors of S

• 2022 ACM SIGPLAN Programming Languages Software Award
• 2021 ACM Software System Award

Airbus

• Development of Level A controllers for A340/600 series
• 70% of code generated automatically
• Quick management of requirements changes
• Major productivity improvement (new project = software $\times$ 2)
• Esterel SCADE has been adopted for most of on-board computers of the A380

What are formal methods?

Specification

• Giving precise statement of what the system must do while avoiding constraints on how it is achieved

Example: everybody should be happy

• Informal specifications are often ambiguous and imprecise

Example: Compute factorial of n

• Formal specification is a mathematical object. One can analyse it, manipulate it, reason about it

Example: PRECOND: $n \in \mathbb{N}$ POSTCOND: returned value is $n!$

Formal methods

• Formal methods allow to mathematically reason about systems

Example: \(\lbrace n \in \mathbb{N}\rbrace \ \texttt{ def fact(n): return 1 if n == 0 else n * fact(n-1) } \ \lbrace r=n!\rbrace\)

• Problem: formal specifications are typically large (thousands of lines)
• Automatic techniques are crucial to be able to analyse real-life systems

Automatic verification is impossible

Program termination is not decidable (Alan Turing, 1936) There is no algorithm to decide if a Turing Machine stops on the empty input

Hence, verification should be:

• either incomplete,
• or not fully automatic

Methods of system verification

Peer reviewing

• Manual code inspection
• On average 60% of errors caught
• Subtle errors (concurrency, algorithm defects) hard to catch
• Used in 80% of all software engineering projects
• Refinement of this method: parallel developpement

Testing

• 30%-50% of development cost
• Programmers have to provide insights what to test, and what should be system response
• When to stop testing?
• Formal specifications help here:
  • One of the most cost-effective uses of formal specifications
  • New tools provide as good coverage as manual test cases, and they avoid programming test cases

Theorem proving

• Doing large proofs semi-automatically

Example: Induction proof, Floyd \& Hoare style proof

PRECOND: $n \in \mathbb{N}$ POSTCOND: $return = n!$

def fact(n):
  return 1 if n == 0 else n * fact(n - 1)

$\frac{\lbrace n=0\rbrace \ \texttt{fact(0)} \ \lbrace 1 = 0!\rbrace \quad \lbrace n > 0 \, \land \, fact(n-1) = (n-1)!\rbrace \ \texttt{fact(n)} \ \lbrace n * fact(n-1) = n!\rbrace}{\lbrace n \in \mathbb{N}\rbrace \ \texttt{def fact(n): return 1 if n == 0 else n * fact(n-1)} \ \lbrace return = n!\rbrace}$

Model-checking

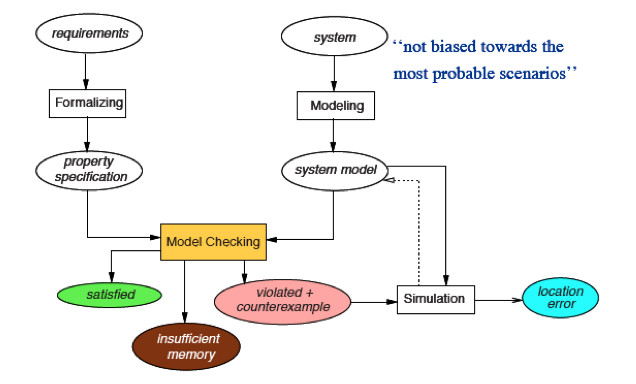
• inputs: finite state model of the system + set of required properties
• makes formal methods available to broad audience

Finite state model

Properties

• The program terminates
• The programe does not terminate
• The computed value is correct
• A sequence of events is correct
• Mutual exclusion
• No deadlock
• No starvation

Pros vs. Cons of model-checking

• Advantages:
  • Widely applicable
  • Ensure specifications are correct before the system is built
  • Fully automatic
  • Produces counterexample
  • Sound and interesting mathematical foundations
• Drawbacks
  • Analyses of an abstraction of the system
  • Focused on control and not data oriented applications
  • High algorithmic complexity

Milestones towards model-checking

• Mathematical program correctness: Church, Turing (1949)
• Syntax-based techniques for sequential programs: Floyd, Hoare (1969)
• Invariant method and program refinment: Dijkstra, Hoare (70’s)
• Program logics (70’s)
  • Algorithmic and dynamic logics
  • Hoare logic
  • Linear temporal logic
• Model-checking using temporal logics: Clarke \& Emerson (1981), Sifakis (same time)
  • ACM Turing award 2007 “…highly effective verification technology…”

Get bugs as soon as you can

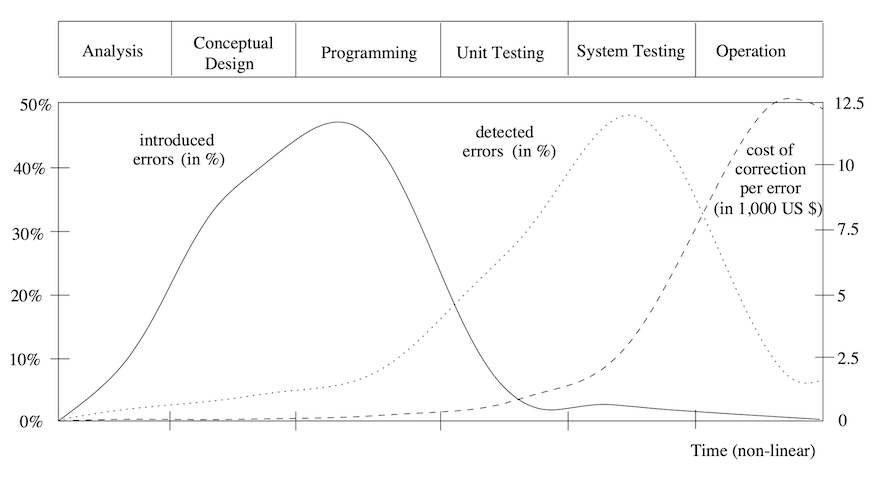
(source: “Principe of Model-Checking”, C. Baier and J.P. Katoen, 2007)

Conclusion

Summary

• Any verification using model-based techniques is only as good as the model of the system (abstraction)
• Formal methods are not silver bullet to eliminate errors
• They are not beyond budget of developers
• They are the only practical means to demonstrate the absence of undesired behaviour
• The process of developing a specification is often the most valuable phase

Who uses formal methods?

• Microsoft Azure (cloud computing)
• Amazon S3 (cloud computing)
• MongoDB Inc (Mongo DB replication protocol)
• Elastic (Elastic search replication protocol)
• Intel (processors)
• Airbus / Dassault (aircrafts, systems 3DS)
• ConsenSys (blockchain, smart contracts)
• Oracle (“Parfait” static analysis)
• Framatome (nuclear reactors)
• Bosch (automotive)
• …

What is next?

• Test vs. Model-checking vs. Proof
• Modelling and abstraction with TLA+
• Specification and verification
• Formal design of programs
• Detecting and solving bugs using model-checking