Temporal specifications

Temporal specifications

Frédéric Herbreteau, Bordeaux INP/LaBRI (frederic.herbreteau@bordeaux-inp.fr)

Objective

• Use model-checking to assert the correctness of a system
  • from a model $M$: a set of runs given as a transition system
  • and a specification $\varphi$ \(M \models \varphi\)
• The specification $\varphi$ shall specify which runs are correct and which are not
• A dedicated algorithm is then use to decide wether $M \models \varphi$ or not

Not all specifications are invariant properties

Specifications and properties

What is a specification?

• Property of the runs of a system: which runs are correct and which are not?
• Must have a clear and well-defined semantics

Example: mutual exclusion

”$\textcolor{blue}{P_1}$ and $\textcolor{red}{P_2}$ do not access the critical section simultaneously”

Formalising specifications

• $AP$ = set of atomic propositions on states (labels)
• $\Sigma = 2^{AP}$ is the set of all sets of atomic propositions (observations)
• $\Sigma^*$ and $\Sigma^\omega$ are the sets finite and infinite sequences over $\Sigma$
• A property $P$ is any subset of infinite traces from $\Sigma^\omega$

Example: mutual exclusion (cf. previous slide)

• $AP$?
• What is $\Sigma$?
• Give some traces from $\Sigma^*$ From $\Sigma^\omega$?
• Express “$\textcolor{blue}{P_1}$ and $\textcolor{red}{P_2}$ do not access the critical section simultaneously”

Temporal properties

• Temporal refers to logical time
• Temporal properties express requirements over infinite sequences of states

Example:

• “Accesses to the critical section are alternatively granted to $\textcolor{blue}{P_1}$ and $\textcolor{red}{P_2}$”
• “If $\textcolor{blue}{P_1}$ requests the critical section, then access is eventually granted”

• A temporal property is true for a model if all its runs satisfy the property
• Two kinds of temporal properties: safety and liveness

Safety properties - “Nothing bad will never happen”

Example:

• Invariant properties are a special case of safety properties
• Partial correcteness for sequential programs
• ”$\textcolor{blue}{P_1}$ and $\textcolor{red}{P_2}$ do not access the critical section simultaneously”
• “Accesses to the critical section are alternatively granted to $\textcolor{blue}{P_1}$ and $\textcolor{red}{P_2}$”

A safety property is characterised by a set $B \subseteq \Sigma^*$ of finite counter-examples

Definition A set $P \subseteq \Sigma^\omega$ is a safety property if there exists a set $B \subseteq \Sigma^*$ of finite counter-examples such that $P = \Sigma^\omega - (B \Sigma^\omega)$

Liveness properties - “Something good will eventually happen”

Example:

• Termination for sequential program
• “Each process will eventually enter the critical section”
• “If $\textcolor{blue}{P_1}$ requests the critical section, then access is enventually granted”
• “Processes enter the critical section infinitely often”

A liveness property is characterised by infinite counter-examples.

Definition: $P \subseteq \Sigma^\omega$ is a liveness property if every finite sequence can be extended into an infinite sequence in $P$

Example: mutual exclusion

Safety: “nothing bad never happens” - finite counter-examples Liveness: “something good eventually happens” - infinite counter-examples

Example: Processes compete to access their critical sections protected by a lock.

Safety of liveness?

• Two processes never access their critical section at the same time
• Each process accesses the critical section infinitely often
• If a process requires access to the critical section, access is eventually granted
• The lock is never stolen

Decomposition of specifications

Decomposition lemma: For every property $P \subseteq \Sigma^\omega$, there exists a safety property $S$ and a liveness property $L$ such that $P = S \cap L$.

Proof: let $Closure(P)$ be the set of words $w \in \Sigma^\omega$ s.t. all their prefixes are prefixes of words in $P$. Then, choose $S = Closure(P)$ and $L = P \cup (\Sigma^\omega - Closure(P))$

Exercise: which properties are safety and liveness at the same time?

• Specifications mix safety, to ensure good behavior, and liveness, to ensure progress
• For sequential programs: correctness (w.r.t. precondition and postcondition) and termination

Temporal Logic

Temporal formulas

$\varphi ::= p \,

\, \lnot \varphi \,

\, \varphi \land \varphi \,

\varphi \lor \varphi \,

\, \varphi \implies \varphi \,

\, \Box \varphi \,

\, \Diamond \varphi \qquad\qquad \text{with } p \in AP$

• $\Box$ means “always”
• $\Diamond$ means “eventually”

Example:

• $\Box \lnot (\textcolor{blue}{cs_1} \land \textcolor{red}{cs_2})$
• $\Diamond \textcolor{blue}{cs_1} \land \Diamond \textcolor{red}{cs_2}$
• $\Box (\textcolor{blue}{req_1} \implies \Diamond \textcolor{blue}{cs_1})$

Semantics of temporal formulas

Expressed over infinite sequences of observations (sets of labels):

Example: labels ${\textcolor{blue}{cs_1}$, $\textcolor{red}{cs_2}}$ trace: {} {} {$\textcolor{blue}{cs_1}$} {} {$\textcolor{red}{cs_2}$} {} {} … {} {$\textcolor{red}{cs_2}$} {} {$\textcolor{blue}{cs_1}$} {} {} {$\textcolor{blue}{cs_1}$, $\textcolor{red}{cs_2}$} {} {} …

$\sigma$ an infinite trace, $\sigma[i]$ its value in $i$, $\sigma[i…]$ its suffix from $i$

• $\sigma \models p$ if $p \in \sigma[1]$
• $\sigma \models \lnot \varphi$ if $\sigma \not\models \varphi$
• $\sigma \models \varphi_1 \land \varphi_2$ if $\sigma \models \varphi_1$ and $\sigma \models \varphi_2$
• $\sigma \models \Box \varphi$ if $\sigma[i…] \models \varphi$ for every $i \ge 1$
• $\sigma \models \Diamond \varphi$ if there exists $i \ge 1$ such that $\sigma[i…] \models \varphi$

Illustration

Example: Labels: ${\textcolor{blue}{req_1}, \textcolor{blue}{cs_1}, \textcolor{red}{cs_2}}$

Traces:

• $\sigma_1$: {} {} {$\textcolor{blue}{cs_1}$} {} {$\textcolor{red}{cs_2}$} {} {} … {} {$\textcolor{red}{cs_2}$} {} {$\textcolor{blue}{cs_1}$} {} {} {$\textcolor{blue}{cs_1}$, $\textcolor{red}{cs_2}$} {} {} …
• $\sigma_2$: {} {$\textcolor{blue}{cs_1}$} {} {} {$\textcolor{red}{cs_2}$} {$\textcolor{blue}{req_1}$} {} {} {} {$\textcolor{blue}{cs_1}$} {} … {} {$\textcolor{blue}{req_1}$} {} {$\textcolor{red}{cs_2}$} {} {} {} {} …

Are the formulas below satisfied or not by the traces above?

• $\Box \lnot (\textcolor{blue}{cs_1} \land \textcolor{red}{cs_2})$
• $\Diamond \textcolor{blue}{cs_1} \land \Diamond \textcolor{red}{cs_2}$
• $\Box (\textcolor{blue}{req_1} \implies \Diamond \textcolor{blue}{cs_1})$

Combining operators

• $\Box\Diamond$ “infinitely often”
• $\Diamond\Box$ “almost always”
• $\rightsquigarrow$ “leads-to” (~> in TLA+): $\varphi_1 \rightsquigarrow \varphi_2$ is a shortcut for $\varphi_1 \implies \Diamond \varphi_2$

Example: Write traces that satisfy the formulas below, and traces that falsify them:

• $\Box\Diamond \textcolor{blue}{cs_1}$
• $\Diamond\Box \textcolor{blue}{req_1}$
• $\textcolor{blue}{req_1} \rightsquigarrow \textcolor{blue}{cs_1}$
• $\Box (\textcolor{blue}{req_1} \rightsquigarrow \textcolor{blue}{cs_1})$

Relation between $\Box$ and $\Diamond$

Exercise: Give traces that are respectively satisfied by $\Box p$, $\Box \lnot p$, $\lnot \Box p$, $\Diamond p$, $\Diamond \neg p$, $\neg \Diamond p$

• What is the difference between $\Box \lnot p$ and $\lnot \Box p$?
• What is the difference between $\Diamond \lnot p$ and $\lnot \Diamond p$?
• What is the relation between $\Box$ and $\Diamond$?

Semantics over a transition system

Definition A transition system $M$ satisfies a temporal formula $\varphi$ ($M \models \varphi$) if $\sigma \models \varphi$ for every infinite trace $\sigma$ from an initial state of $M$.

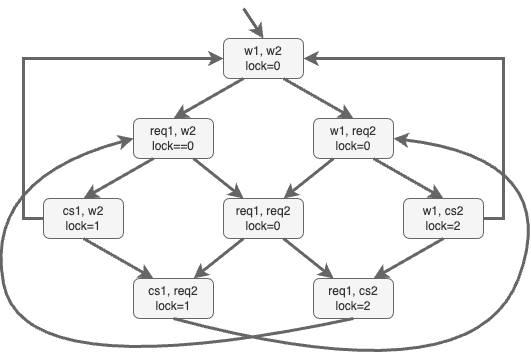
Example: Which formulas below are satisfied by the model to the right?

• $\Box \lnot (\textcolor{blue}{cs_1} \land \textcolor{red}{cs_2})$
• $\Diamond \textcolor{blue}{cs_1} \land \Diamond \textcolor{red}{cs_2}$
• $\Box (\textcolor{blue}{req_1} \implies \Diamond \textcolor{blue}{cs_1})$

Temporal formulas in TLA+

• Corresponding TLA+ operators: ~, /\, \/, =>, [], <>

• Specification of temporal formulas:

NoStarvation == [](req1 ~> cs1)   (* in the .tla file *)

PROPERTY NoStarvation             \* in the .cfg file