Algorithmic verification

Algorithmic verification

Frédéric Herbreteau, Bordeaux INP/LaBRI (frederic.herbreteau@bordeaux-inp.fr)

Objective

  • Use model-checking to assert the correctness of a system
    • from a model $M$: a set of runs given as a transition system
    • and a specification $\varphi$ \(M \models \varphi\)
  • The specification $\varphi$ shall specify which runs are correct and which are not
  • A dedicated algorithm is then use to decide wether $M \models \varphi$ or not

Verification of invariance properties

Algorithmic verification of invariance properties

  • Invariance properties that involve only one state (not a sequence of states)
  • Must hold in every state of the model

Example:

  • mutual exclusion: no state with both $\textcolor{blue}{cs_1}$ and $\textcolor{red}{cs_2}$

Exercise: Give an algorithm to check an invariance property over a finite transition system

Verification of temporal properties

Temporal formulas

$\varphi ::= p \, \vert \, \lnot \varphi \, \vert \, \varphi \land \varphi \, \vert \, \varphi \lor \varphi \, \vert \, \varphi \implies \varphi \, \vert \, \Box \varphi \, \vert \, \Diamond \varphi \qquad\qquad \text{with } p \in AP$

  • $\Box$ means “always”
  • $\Diamond$ means “eventually”

Example:

  • $\Box \lnot (\textcolor{blue}{cs_1} \land \textcolor{red}{cs_2})$
  • $\Diamond \textcolor{blue}{cs_1} \land \Diamond \textcolor{red}{cs_2}$
  • $\Box (\textcolor{blue}{req_1} \implies \Diamond \textcolor{blue}{cs_1})$

TLA+ operators: ~, /\, \/, =>, [], <>

Semantics of temporal formulas

Expressed over infinite sequences of observations (sets of labels):

Example: labels ${\textcolor{blue}{cs_1}$, $\textcolor{red}{cs_2}}$ trace: {} {} {$\textcolor{blue}{cs_1}$} {} {$\textcolor{red}{cs_2}$} {} {} … {} {$\textcolor{red}{cs_2}$} {} {$\textcolor{blue}{cs_1}$} {} {} {$\textcolor{blue}{cs_1}$, $\textcolor{red}{cs_2}$} {} {} …

$\sigma$ an infinite trace, $\sigma[i]$ its value in $i$, $\sigma[i…]$ its suffix from $i$

  • $\sigma \models p$ if $p \in \sigma[1]$
  • $\sigma \models \lnot \varphi$ if $\sigma \not\models \varphi$
  • $\sigma \models \varphi_1 \land \varphi_2$ if $\sigma \models \varphi_1$ and $\sigma \models \varphi_2$
  • $\sigma \models \Box \varphi$ if $\sigma[i…] \models \varphi$ for every $i \ge 1$
  • $\sigma \models \Diamond \varphi$ if there exists $i \ge 1$ such that $\sigma[i…] \models \varphi$

Semantics over a transition system

Definition A transition system $M$ satisfies a temporal formula $\varphi$ ($M \models \varphi$) if $\sigma \models \varphi$ for every infinite trace $\sigma$ from an initial state of $M$.

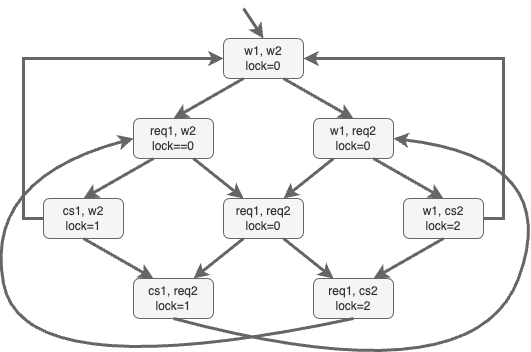
Example: Which formulas below are satisfied by the model to the right?

  • $\Box \lnot (\textcolor{blue}{cs_1} \land \textcolor{red}{cs_2})$
  • $\Diamond \textcolor{blue}{cs_1} \land \Diamond \textcolor{red}{cs_2}$
  • $\Box (\textcolor{blue}{req_1} \implies \Diamond \textcolor{blue}{cs_1})$

bg right:40% fit

Algorithmic verification of temporal formulas (overview)

Goal: given $M$ and $\varphi$, decide whether $M \models \varphi$

Algorithm:

  1. From $\varphi$ compute a Büchi automaton $\mathcal{A}_{\lnot \phi}$
  2. Compute the product $\mathcal{B} = M \otimes \mathcal{A}_{\lnot \phi}$
  3. Decide whether $\mathcal{L}(\mathcal{B}) = \emptyset$

From TL formulas to Büchi automata

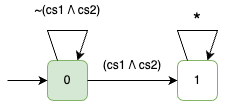
Example: $\Box \lnot (\textcolor{blue}{cs_1} \land \textcolor{red}{cs_2})$

  • {} {$\textcolor{blue}{cs_1}$} {} {} {$\textcolor{red}{cs_2}$} {} {$\textcolor{blue}{cs_1}$} {} {} …
  • {} {} {$\textcolor{red}{cs_2}$} {} {$\textcolor{blue}{cs_1}$, $\textcolor{red}{cs_2}$} {} {$\textcolor{blue}{cs_1}$} {} …

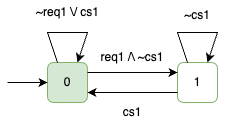
Example: $\Box (\textcolor{blue}{req_1} \rightsquigarrow \textcolor{blue}{cs_1})$

  • {} {$\textcolor{blue}{req_1}$} {} {} {$\textcolor{blue}{cs_1}$} {} {$\textcolor{blue}{cs_1}$} {} {} {$\textcolor{blue}{req_1}$, $\textcolor{blue}{cs_1}$} {} …
  • {} {} {$\textcolor{blue}{req_1}$} {$\textcolor{blue}{cs_1}$} {} {$\textcolor{blue}{req_1}$} {} {} {$\textcolor{blue}{req_1}$} {} {}…

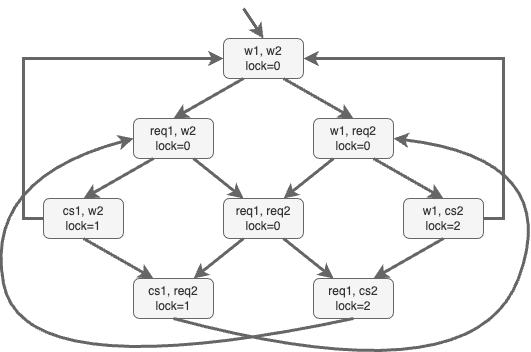
bg vertical right:33% fit bg right:33% fit

Product $M \otimes \mathcal{A}_{\lnot \varphi}$ (1/2)

Example: $\Box \lnot (\textcolor{blue}{cs_1} \land \textcolor{red}{cs_2})$

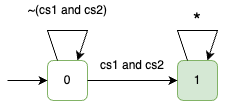
Product $M \otimes \mathcal{A}_{\lnot \varphi}$ (2/2)

Example: $\Box (\textcolor{blue}{req_1} \rightsquigarrow \textcolor{blue}{cs_1})$

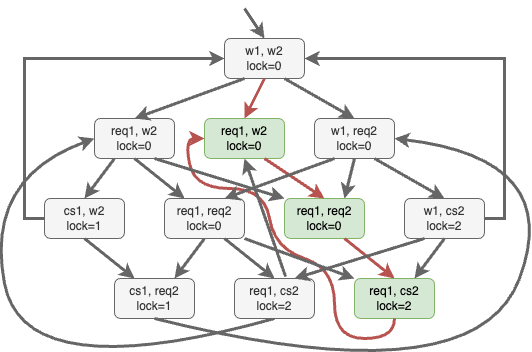
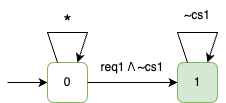
Checking if $\mathcal{L}(M \otimes \mathcal{A}_{\lnot \varphi}) = \emptyset$

  • $\mathcal{L}(M \otimes \mathcal{A}_{\lnot \varphi}) \neq \emptyset$ iff there is an infinite run that visits an accepting state infinitely many times

  • What is the structure of a such a run?

Exercise: give an algorithm that decides if $\mathcal{L}(M \otimes \mathcal{A}_{\lnot \varphi}) \neq \emptyset$

  • How to include fairness constraints in the model-checking process?

Complexity

Theorem: the TL model-checking problem is PSPACE-complete

Overall complexity of the verification algorithm:

  • TL to Büchi automaton: $\vert \mathcal{A}_{\lnot \varphi} \vert = 2^{\mathcal{O}(\vert \varphi \vert)}$
  • Product: $\vert M \otimes \mathcal{A}{\lnot \varphi} \vert = \mathcal{O}(\vert M \vert \times \vert \mathcal{A}{\lnot \varphi} \vert)$
  • Emptiness checking: $\mathcal{O}(\vert M \otimes \mathcal{A}_{\lnot \varphi} \vert)$
  • Overall complexity: $\mathcal{O}(\vert M \vert \times 2^{\vert \varphi \vert})$